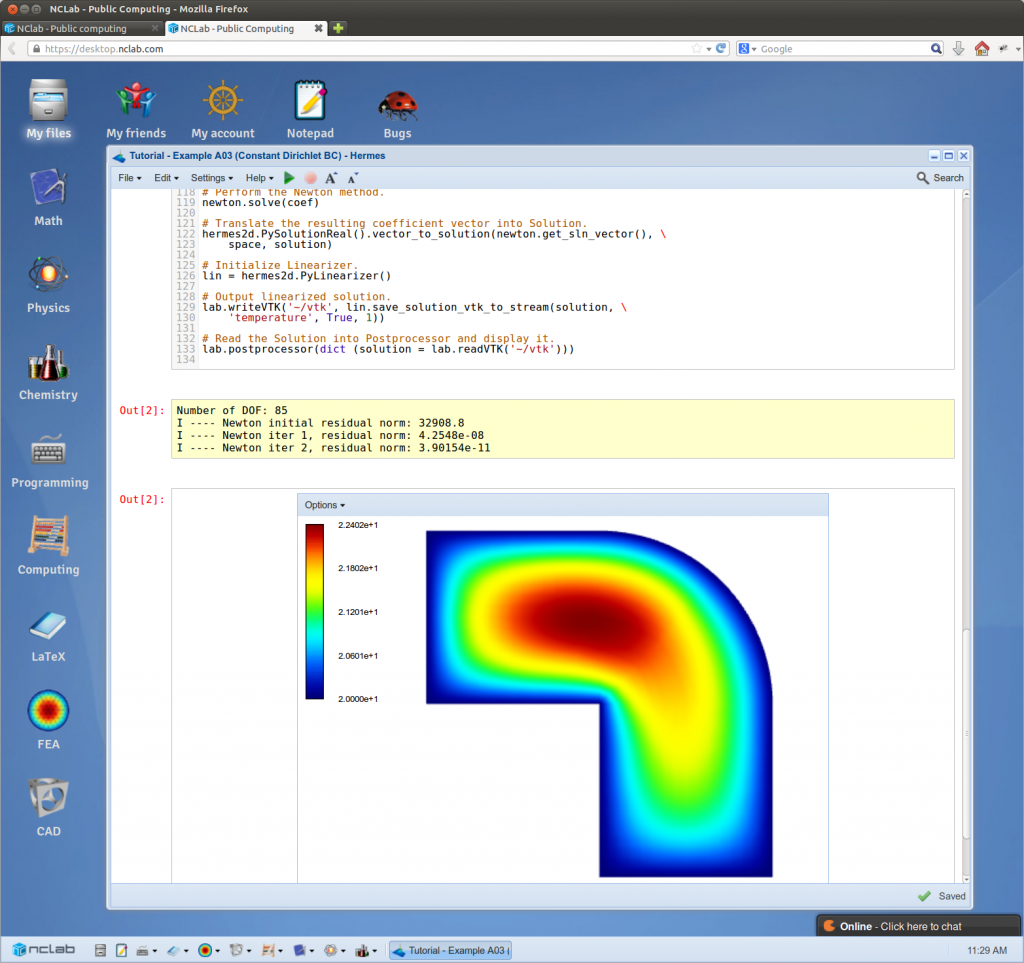
 The Hermes finite element library is now completely wrapped in Python and available in the Computing section of NCLab. This means that NCLab users can write their own advanced FEM programs using higher-order elements, automatic adaptivity, and other cool features of Hermes. The wrappers follow very closely the C++ version of the library, so C++ tutorial and library documentation can be used. Several tutorial examples were translated to Python and are available as displayed projects in NCLab (look for “Hermes – Tutorial – …”). We also wrote a tutorial to the Python wrappers and examples showing how NCLab Gemoetry Editor, Mesh Editor and Postprocessor can be connected to Hermes codes (look for displayed projects whose name starts with “GE and ME”).
The Hermes finite element library is now completely wrapped in Python and available in the Computing section of NCLab. This means that NCLab users can write their own advanced FEM programs using higher-order elements, automatic adaptivity, and other cool features of Hermes. The wrappers follow very closely the C++ version of the library, so C++ tutorial and library documentation can be used. Several tutorial examples were translated to Python and are available as displayed projects in NCLab (look for “Hermes – Tutorial – …”). We also wrote a tutorial to the Python wrappers and examples showing how NCLab Gemoetry Editor, Mesh Editor and Postprocessor can be connected to Hermes codes (look for displayed projects whose name starts with “GE and ME”).
11/26/2023