In 3D Modeling, by Boolean operations we mean creating intersections and unions of objects, as well as subtracting objects from each other. All these are set operations that students know from Venn diagrams. Let’s stay with the last one for the moment. In order to demonstrate subtraction, let’s consider a pair of overlapping objects, such as a cylinder and a cube:
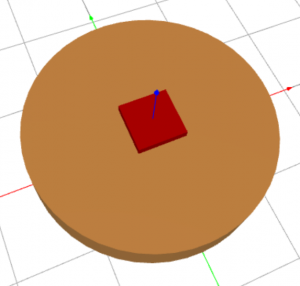
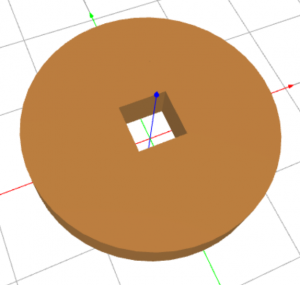
Subtracting the cube from the cylinder is not technically difficult – usually this is done using a single command or mouse click in the 3D modeling software at hand. As a result, one obtains a set of 3D points that belong to the cylinder but not to the cube:
However, Boolean operations become tricky when complex objects are involved. Let’s have a look at this spoked wheel which is an extension of the hollow cylinder that we just made:

The wheel can be built in many different ways. Let’s consider two. First, let’s (1) create the interior cylinder, (2) subtract the cube from it and (3) create a union with the spokes and the rim. Exactly the same result can be obtained by (1) creating a union of the interior cylinder, the spokes, and the outer rim and (2) subtracting the cube from it. However, one of these two approaches will be significantly computationally simpler and faster than the other. Can you guess which one it is?
Before we answer, let’s understand how the subtraction works. It is an operation between 3D objects. The surface of each object is defined via certain number of faces. The algorithm analyses the interaction of all faces of one object with all faces of the other object. Therefore, the computational complexity increases rapidly when objects have a large number of faces.
In the former approach, the subtraction occurs between two relatively simple objects – a cylinder and a cube. In the latter, the cube is subtracted from a much more complex object that is formed by the inner cylinder, 16 cylindrical spokes, and the outer rim. Therefore, the former approach is computationally much more efficient. In concrete numbers, the CPU time for the former approach was 1.9 s while the latter approach took 5.4 s which is almost three times more.
The conclusion of this simple experiment is that the order of Boolean operations matters. If subtraction is needed, then it is a good idea to do it as soon as possible, between as simple shapes as possible. Subtracting complex objects can be extremely costly in terms of CPU time.