NCLab’s new self-paced online 3D modeling course was first tested today in our afterschool program for 4-5 graders at the Roy Gomm Elementary School in Reno. Our fear that kids would find the games boring or too challenging, or that they would not like typing code, was quickly dissolved. THEY LIKED IT! Amazingly, they did
CUE is our favorite event – we always meet many teachers who are enthusiastic about STEM and eager to learn new things. NCLab is a bottomless resource for such creative minds. This year, Fall CUE took place at American Canyon High School which is located close to Napa. Certainly one of the largest and fanciest high
NCLab was presented tonight at a STEM Night organized by the Hug High School in Reno. As usual, we were the only table related to computer programming and 3D modeling. The interest of both the kids and the parents was enormous. Here is Brad, the first NCLab’s Program Manager. Awesome communicator and great organizer, with
In September 2014 we completed the first round of after school programs in Reno, trained teachers in Mineral County SD, hosted K-12 school workshops at UNR, and added lots of new functionality to NCLab. First Round of After School Programs Completed! The first month of NCLab computer programming and 3D modeling after school programs in
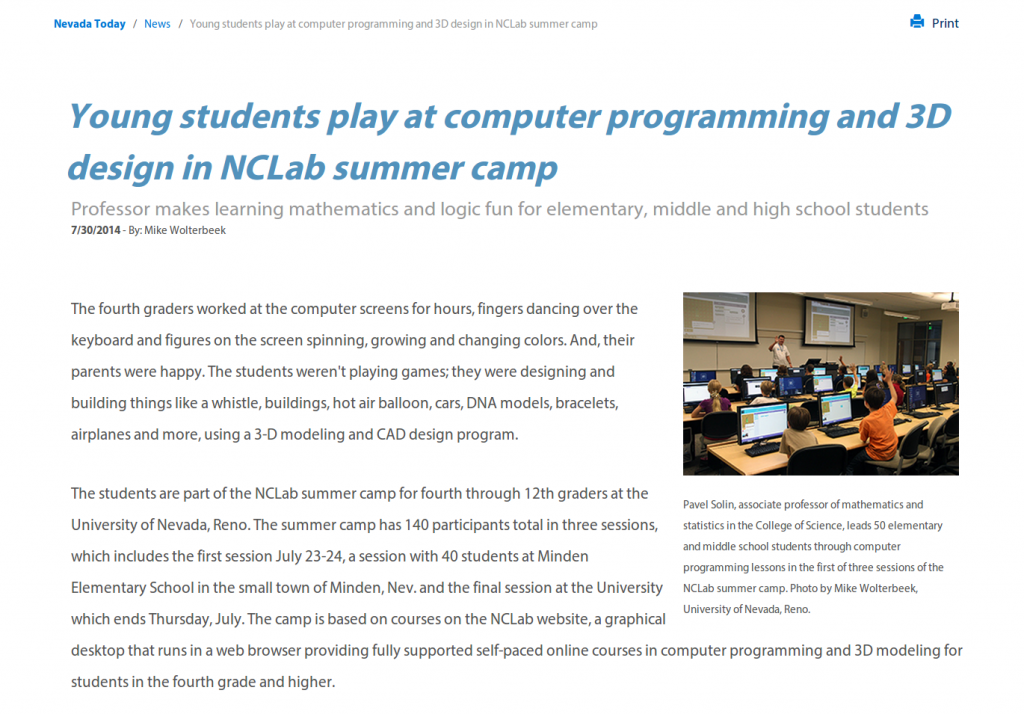
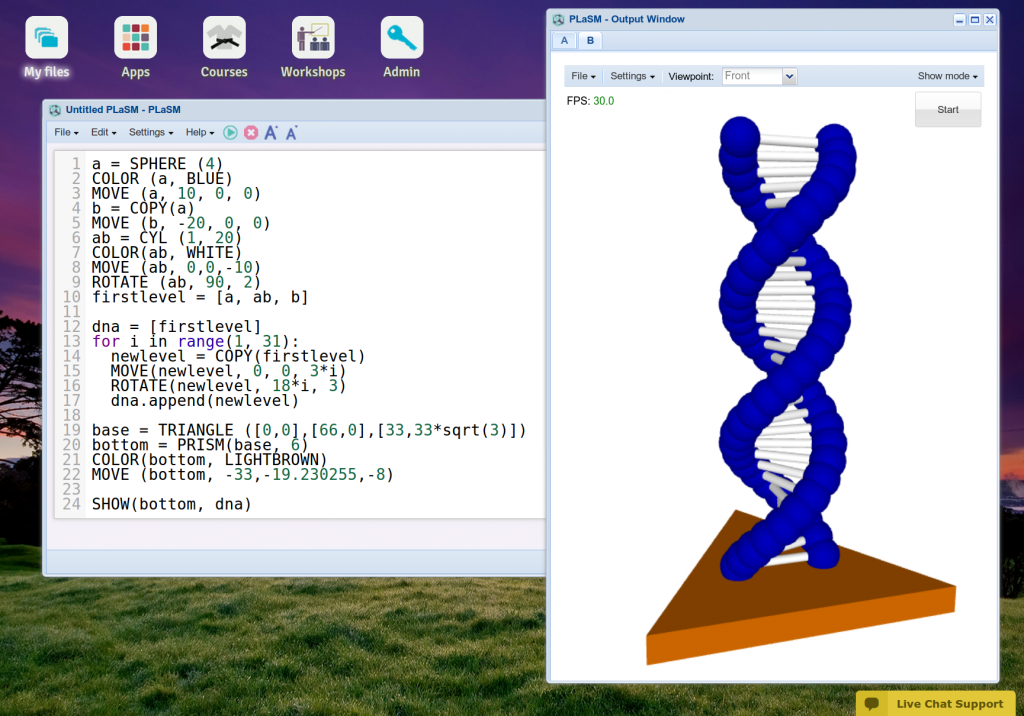
Growing Demand The demand for Computer Programming and 3D Printing (CAD Modeling) instruction using NCLab is growing. While the NCLab Summer Camp 2013 had 50 students and was full, the NCLab Summer Camp 2014 had 150 students and there was still much more demand. Many parents have asked about instruction that we offer during the
New version of NCLab’s self-paced 3D Printing Course with many improvements and new design projects is coming in October 2014. Besides lots of 3D geometry and CAD modeling it will be lots of fun – see few sample screenshots below. Remember that every K-12 school is eligible for 10 free student accounts with access to
NCLab is proud to announce a partnership with a Reno-based non-profit organization 360 Blueprint. The mission of 360 Blueprint is to build a collaborative of community churches, public schools, law enforcement agencies, University, and community college students, high school students, community volunteers, and families to transform the lives of the youth in the Washoe County
Aerotek is a firm that provides engineering, design and specialty personnel services to companies such as NV Energy. NCLab attracted the attention of Aerotek because it gets kids excited about engineering at an early age, and because it gives them real math and engineering skills in a very accessible form through self-paced online courses, summer
An article about this year’s NCLab Summer Camps was recently published in Nevada Today (click here to view the original article).
Coder Dojo in NYC (CDNYC) is a non-profit organization that offers free computer programming courses to 7 – 17 old students. Vaibhav Verma of CDNYC says: “The simplicity of the Karel environment helps students learn problem solving without distractions. It also eases its way into “real” programming languages a lot more easily than other approaches.”